Unterrichtsmaterialien Mathematik: Graphen
17 MaterialienIn über 17 Dokumenten und Arbeitsblättern für das Fach Mathematik: Graphen findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Auswählen
Auswählen
Auswählen
Auswählen
17 Materialien
Einheit
Mint Zirkel - Ausgabe 02, Juni 2017Folgende Themen werden mit Praxisbezug vorgestellt: Graphen, erdähnliche Planeten, Mathematik in der Politik, Ausbildung zum Fluglotsen, Neudefinition des Kilogramms durch eine Siliziumkugel, die Vermessung der Welt, moderne Labortechnik, kollaboratives Arbeiten mit digitalen Medien, Projekttag zur Demenzform Alzheimer, MINT-Schülerwettbewerbe, Dynamikum, Lehrergesundheit und Astronauten.
Analysis
5-13. Klasse
Berufliche Schule
15 SeitenAnalysis5-13. KlasseBerufliche Schule15 SeitenTesten kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
Einheit
PotenzfunktionenPotenzfunktionen mit positiven Exponenten; Potenzfunktionen mit negativen Exponenten; Veränderungen am Graphen - Streckung und Stauchung in y-Richtung und Spiegelung an der x-Achse; Veränderungen am Graphen - Verschiebung in y-Richtung und x-Richtung; Vermischte Aufgaben
Ableitung7-10. KlasseGymnasium17 SeitenAbleitung7-10. KlasseGymnasium17 Seiten
Einheit
GraphenReise nach Rio – Klimadiagramme lesen; Eine Fieberkurve zeichnen und interpretieren; Füllkurven-Puzzle
Graphen7. KlasseSekundarstufe 13 SeitenGraphen7. KlasseSekundarstufe 13 Seiten
Einheit
Einführung in die ZuordnungenStation 1: Zuordnungen – immer eindeutig? Station 2: Je mehr – desto …; Station 3: Zuordnungen erkennen und ergänzen; Station 4: Graphen interpretieren I; Station 5: Graphen interpretieren II; Station 6: Graphen zuordnen; Station 7: Graphen zeichnen; Lernzielkontrolle: Einführung in die Zuordnungen
Analysis6-10. KlasseSekundarstufe 111 SeitenAnalysis6-10. KlasseSekundarstufe 111 SeitenVerwandte Themen
Einheit
Teil I: „Graphen“, „Wege in Graphen“ – einige GrundbegriffeWo geht’s denn hier zu ...?; Was ist ein „Graph“?; Wege in Graphen
Graphen10-13. KlasseGesamtschule3 SeitenGraphen10-13. KlasseGesamtschule3 Seiten
video
Lineare Gleichungen - grafische DarstellungWie kann man lineare Gleichungen grafisch darstellen? Das Verfahren ist ganz einfach: Es wird gezeigt, wie man Wertepaare aus einer Tabelle in das Koordinatensystem überträgt. Die Funktionsvorschrift der linearen Funktion wird erläutert, und anhand von Beispielen werden unterschiedliche Graphen gezeichnet.
Analysis5-13. KlasseGesamtschuleAnalysis5-13. KlasseGesamtschule
Einheit
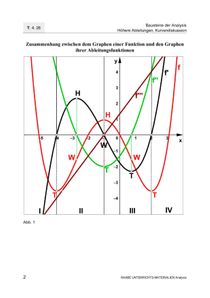
Zusammenhang zwischen dem Graphen einer Funktion und den Graphen ihrer AbleitungsfunktionenZusammenhang zwischen dem Graphen einer Funktion und den Graphen ihrer Ableitungsfunktionen
Graphen11-13. KlasseBerufliche Schule10 SeitenGraphen11-13. KlasseBerufliche Schule10 Seiten
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner
Probezeit, entstehen für dich keine Kosten. 🚀
Probezeit, entstehen für dich keine Kosten. 🚀
